Evaluar Limites De Integracion

Por lo que podemos utilizar la fórmula. Posteriormente se evalúa el resultado de la integral restando el valor obtenido al sustituir el límite de integración inferior al del obtenido al sustituir el límite de integración superior.

La Integral Definida Calculo21

Integrar funciones que involucran funciones logarítmicas.

Evaluar limites de integracion. Tan loco como suena podemos de hecho calcular algunas integrales impropias mediante métodos ingeniosos que involucran límites. A y b son el límite inferior y el límite superior de la integración y definen el dominio de integración. Los límites de integración deben concondar con la variable a estudiar es decir si se realiza un cambio de variable se deben cambiar los límites Se debe evaluar la función resultante sustituyendo los límites superior menos inferior como se puede ver en la figura es por la diferencia.

Entre otras cosas nos permiten calcular el volumen bajo. La integral definida entre dos límites de integración iguales es decir cuando el límite superior de integración y el límite inferior son iguales entonces su resultado es igual a cero. La integral cartesiana se convierte entonces en donde G representa la misma región de integración descrita ahora en coordenadas polares.

Esta es la fórmula de integración por partes. La Calculadora de Integrales te permite calcular en línea integrales y antiderivadas de funciones Gratis. Evaluar integrales definidas por propiedades algebraicas.

La diferencia entre estos valores es el valor de la integral definida. Por tanto ZZ R x2y2 dx dy 1 2 Z 2 1 u2 du Z 4 1 dv v 7 6 lnv 4 1 7 6 ln4 7 3 ln2. En los dos ejemplos anteriores ya estaban dados los límites de integración por tanto no había más que aplicar el teorema de Fubini para evaluar las integrales dobles pero en otras ocasiones es necesario identificar la región de integración porque los límites no están definidos.

B es el límite superior de la integración. Luego obtenemos los límites de integración de ambas coorde-nadas polares para la frontera de R. A Displaystyle a y.

Es el integrando o función a integrar. Explicación paso a paso. Esto es como el método de sustitución del capítulo 5 excepto que ahora se sustituyen dos va-.

Aprende cómo se logra esto y cómo podemos movernos entre la representación del área como integral definida y como suma de Riemann. Como una integral iterada es simplemente un tipo especial de integral definida en el que el integrando es también una integral se pueden utilizar las propiedades de las. El signo una S alargada representa la integración.

F es el integrando que se tiene que evaluar al variar x sobre el intervalo ab. Ejemplo 1 Calcular xdA R. E fx ex en 02.

L as funciones exponenciales y logarítmicas se utilizan para modelar el crecimiento de una población el crecimiento celular y el crecimiento financiero así como la depreciación la desintegración radiactiva y el consumo de recursos por nombrar solo algunas aplicaciones. Es diferencial de e indica cuál es la variable de la función que se integra. Las integrales impropias son integrales definidas en las cuales uno o ambos límites de integración están en infinito o en las que el integrando tiene una asíntota vertical dentro del intervalo de integración.

Y dx puede tener diferentes interpretaciones dependiendo de la teoría. Para resolver o evaluar una integral definida se calcula la integral sin tomar en cuenta los límites de integración. Integrales Dobles Las integrales dobles son una manera de integrar sobre una región bidimensional.

La primera integral la podemos resolver con la fórmula para integrar una potencia. Te ayuda a practicar mostrándote el procedimiento completo integración paso a paso. Este límite puede calcularse con las fórmulas de integración inmediata.

Método de cambio de variable. Evaluar limites de integracion. Los limites de integración de una integral iterada define dos intervalos para las variables.

Nuestra calculadora te permite verificar tus soluciones a ejercicios de Cálculo. De ahí que en la primera sección de este artículo se examinen. Todas las técnicas comunes de integración e incluso funciones.

Incluyen la integración sobre límites infinitos o. Esta separación obviamente se realizará a través de puntos interiores del intervalo en. Separarla como la suma de tantas integrales impropias como sea necesario de forma que cada una de ellas solamente posea un punto de impropiedad en algún límite de integración.

En cálculo y análisis matemático los límites de integración de la integral. El integrando puede convertirse en infinito dentro de los límites de integración. La integral definida se representa por.

Los las mejores profesores as de matemáticas que están disponibles. Las superficies figura 1530 se cortan en el cilindro elíptico x2 1 3y2 5 8 2 x2 2 y2 o x2 1 2y2 5 4 z. Integrar sumas de funciones.

Ecuaciones de la recta Funciones Aritmética y composición Secciones cónicas Transformación. Cambio de los limites de integracion. Esto es así porque realmente no estamos calculando el área entre dos límites de integración.

A B F X D X Displaystyle int _ a b f x dx de un Riemann integrable función f definida en un cerrada y delimitada intervalo son los números reales. Para obtener los límites de integración y evaluar la in-tegral primero graficamos la región. Las sumas de Riemann nos ayudan a aproximar integrales definidas y también nos ayudan a definirlas formalmente.

Para calcular el valor de la integral definida evaluamos primero el límite superior y después el límite inferior. Sea u fx y v gx. En la integración definida se obtiene un resultado numérico que se obtiene al integrar la expresión dada evaluar los límites y hacer la sumatoria de los resultados obtenidos luego de la evaluación.

La frontera de la región R la pro-. Ecuaciones de la recta Funciones Aritmética y composición Secciones cónicas Transformación. A es el límite inferior de la integración.

Cómo se encuentran los limites de integración. Para que resulte más fácil de recordar se puede utilizar la siguiente notación. Derivadas Aplicaciones de la derivada Limites Integrales Aplicaciones de la integral Aproximación integral Series EDO Cálculo multivariable Transformada de Laplace Serie de TaylorMaclaurin Serie de Fourier.

Con el cambio de variable y notemos que en integrales definidas no es necesaria la constante de integración. Imagine un rayo L que parte del origen y que corta a R en la dirección creciente de r. Para resolver o evaluar una integral definida se calcula.

Es el signo de integración. De esta manera obtenemos Es decir 2.

Escribir El Limite De Una Suma De Riemann Como Una Integral Definida Khan Academy En Espanol Youtube

Pin En Como Integrar

1 2 Propiedades De Los Limites Portafolio Matematico

Pin En Matematica

Como Desarrollar Integrales Aplicando Formas Basicas De Integracion Formas Basicas Trinomio Integral

Grafica De Funciones Polinomiales Polinomios Trigonometria Algebra

Pin En Lagos

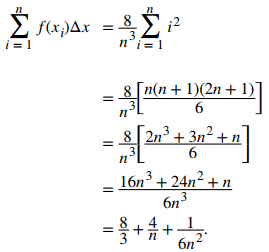
La Integral Definida Calculo21

Ejercicios De Limites Indeterminacion 1 Elevado Infinito Matematica Ensino De Matematica Trigonometria

La Integral Definida De Una Funcion Por Partes Calculo Khan Academy En Espanol Youtube

Limites Trigonometricos Indeterminados Ejercicios Resueltos Fisimat Limites Trigonometricos Calculo De Limites Formulas Matematicas

Pin En College

Integracion Por Fracciones Parciales La Obtencion De La Integral De Una Funcion No Siempre Es Posible Mediante Las Formulas B Fracciones Matematicas Formulas

Pin En Limites

Ejercicios De Limites Matematica Indeterminacion 0 0 Matematicas Matematica Ejercicios Problemas De Razonamiento Logico

Resolver Integrales Impropias Con Uno O Dos Limites Infinitos De Integracion Para Dummies

Ejercicios Resueltos De Derivadas Ejercicios Resueltos Ejercicios Lecciones De Matematicas

Integracion Por Fracciones Parciales Ejercicio 4 Youtube Fracciones Matematicas Ejercicios

Como Resolver Integrales Impropias Que Tienen Uno O Dos Limites Infinitos De Integracion Para Dummies