Formula De Cambio De Variable En Una Integral
Veamos a qué nos referimos encontrando. Por ejemplo si los extremos de la integral inicial con variable x son 0 y 1 y la nueva variable es z 2x entonces los nuevos extremos serán 0 y 2.
Cambios De Variable Recomendados Para Integrales Graficas Matematicas Angulos Matematicas Matematicas Faciles
Entonces para el cambio x g t dx g tdt.

Formula de cambio de variable en una integral. Para convertir una integral de coordenadas x y a s t hacemos. Podemos resolver la integral. Al calcular una integral indefinida la técnica de realiza un cambio de variable o sustitución de variable -substitución a menudo es una manera para hacer que una integral dificil sea más fácil de calcular Una vez que la integración más fácil se realiza para.
Básicamente en la integración por cambio de variable se busca ser más ordenados en la identificación de la diferencial y en revisar si esta está completa o no. Sustituyendo toda la información en la integral obtenemos 1 e x e x d x 1 t 1 t d t t 1 t 2 1 d t arctg t Finalmente deshacemos el cambio de variable para terminar esta integral por sustitución obteniendo 1 e x e x d x arctg e x C. Cambio de variables en integrales múltiples Cambio de variable en integrales dobles En cálculo de una variable se emplea con frecuencia un cambio de variable una sustitución para simplificar una integral.
Hacer un cambio de variable para integrales definidas es muy similar a hacerlo con integrales indefinidas pero con un paso adicional. Tomaremos ahora z. Formula de cambio de variable en una integral.
Al observar que la función exponencial en su exponente genera una derivada y que esta debe estar dentro de la integral. Solucion Cada una de las componentes x u2 4u y v es funcion de una sola variable. Sea D 0101 y se define T.
Una forma de evitar este problema es. La integral por cambio de variable nos ayuda a integrar funciones en donde las fórmulas de integración básicas no son suficientes. Cambio de variables en la integral doble.
X J kmJ k. Todos nuestros vídeos organizados por temáticas. PASOS PARA INTEGRAR POR CAMBIOS DE VARIABLES.
Para calcular la integral resultante realizaremos otro cambio de variable. Un cambio de variables puede ser útil también en las integrales dobles. En general si partimos de una integral conocida f x dx gx k y cambiamos la variable x por la función derivable ux tal que ux es continua obtenemos LA.
D t d x 2. G1B al aplicar el teorema del cambio de variables a la transformacion g y teniendo en cuenta las observaciones anteriores se obtiene la siguiente formula. Un cambio de variable para integrales dobles de gran utilidad es el que corresponde a las coordenadas polares.
Se despeja u y dx sutituyendo en la integral. R2 R2 como Tuv u2 4uv. Los cambios a coordenadas polares esfericas o cilındricas son algunos de los mas empleados.
X cos 2 x 2 3 d x. E x 1 e x 1 t. X2 y2 1.
Método de cambio de variable con integrales definidas. Encontrar D TD. Integral por cambio de variable.
Los siguientes elementos son dignos de toda consideración cuando se piense aplicar este cambio. El método de cambio de variable es un poco más complicado cuando se aplica en integrales definidas porque al cambiar la variable deben actualizarse los extremos de integración. CAMBIO DE VARIABLES EN LA INTEGRAL DOBLE.
Sin embargo en cálculo integral se. En matemáticas cada tipo de problema sugiere un tipo de solución. Primero debemos identificar una sección dentro de la integral con una nueva variable llamémosla.
INTEGRALES DOBLES SOBRE RECTANGULOS. Aplicar el cambio de variables a coordenadas polares x rcosθ y rsenθpara hallar Z A ex 2y dxdy. ƒ x dx f g tg t dt.
Para ver que T es inyectiva basta comprobar que lo son cada una de las componentes. Debemos buscar un cambio de variable que transforme la integral en una integral inmediata o composición de funciones. Cambio de variables en coordenadas polares.
La siguiente integral no se le puede aplicar la integración por partes directamente se tiene que realizar un cambio de variable previo. 1 x 2 4 x 2 d x 2 4 t 2 4 4 t 2 d t 1 4 1 t 2 1 t 2 d t. 1º Se hace el cambio de variable y se diferencia en los dos términos.
Un cambio de variable es básicamente invertir la regla de la cadena. Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t de modo que se obtenga una integral más sencilla. Para calcular la derivada de una función en general el problema es muy sencillo pues solamente se requiere que identifiquemos el tipo de función para saber qué regla fórmula vamos a utilizar para derivarla.
Para cambiar de variable identificamos una parte de lo que se va a integrar con una nueva variable t de modo que se obtenga una integral más sencilla. Observamos que es la derivada de por lo que podemos aplicar un. Un cambio de variable nos ayuda a simplificar una expresión complicada al volver una.
Este método consiste en simplificar la expresión en la integral de modo que tome la forma más semejante posible a las reglas de integración que estudiaste antes. Ejemplo 76 Calcular R D. De una celda como el producto de las longitudes de sus aristas llamaremos suma inferior de fcon respecto a la particion Pa LfP X J kP ınffx.
De acuerdo con la regla de la cadena la derivada de es. Int xcosleft 2x23rightdx xcos2x2 3dx aplicando el método de integración por sustitución o cambio de variable. En un cambio de variable tomamos una expresión de la forma y encontramos su antiderivada.
En esta sección aprenderá a utilizar la técnica de sustitución para definir integrales. En el caso de la integral de Riemann para funciones reales de una variable real se puede demostrar un teorema de cambio de variable de forma muy sencilla utilizando los teoremas fundamentales del calculo en. El método de integración por sustitución o cambio de variable se basa en la derivada de la función compuesta.
Realizaremos primero el cambio de variable t x 2 para eliminar el 4 de dentro de la integral. Tomar en cuenta los límites de integración. El método se resume en encontrar u que se pueda cambiar por toda la función sin exponentes o.
Z B fxydxdy A frcosθrsenθrdrdθ Ejemplo 75 Sea A xy R2. De esta forma se ha transformado el integrando en función de la nueva variable t.
Integral Definida Mediante Cambio De Variable Esquemas Electricos Integral Estudio
Ejercicios Propuestos De Integrales Metodo De Sustitucion O Cambio De Variable Parte 3 Studying Math Algebraic Expressions Physics Books
Pin Em Ejercicios De Integrales
Aplicamos El Cambio De Variable Y Obtenemos La Integral Int 1 Raiz 1 E Z Dz Aprendizaje Matematicas
Aplicamos El Cambio De Variable Y Obtenemos La Integral Int Raiz 4 9 2sin Z 3 2 2cos Z 3 Dz Aprendizaje Matematicas Bachillerato
Ejercicios Propuestos De Integrales Metodo De Sustitucion O Cambio De Variable Parte 1 Math Formulas Math Formula Chart Mathematics
Ejercicios Resueltos Integracion Por Sustitucion O Cambio De Variable Ejercicios Resueltos Aritmetica Trigonometria
Pin Em Ejercicios De Integrales
Differentiation Formulas Calculus Ap Calculus
Aplicamos El Cambio De Variable Y Resolvemos La Integral Obteniendo Z 7 7 Z 5 5 K Lecciones De Matematicas Aprendizaje Matematicas
Aplicamos El Cambio De Variable Y Obtenemos La Integral Int 1 2 3z Dz Aprendizaje Matematicas
Ejercicios Propuestos De Integrales Metodo De Sustitucion O Cambio De Variable Par Calculo Diferencial E Integral Funciones Matematicas Matematica Ejercicios
Aplicamos El Cambio De Variable Y Resolvemos La Integral Obteniendo Z 5 5 Z 3 3 K Aprendizaje Matematicas






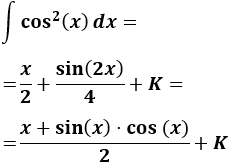
Post a Comment for "Formula De Cambio De Variable En Una Integral"